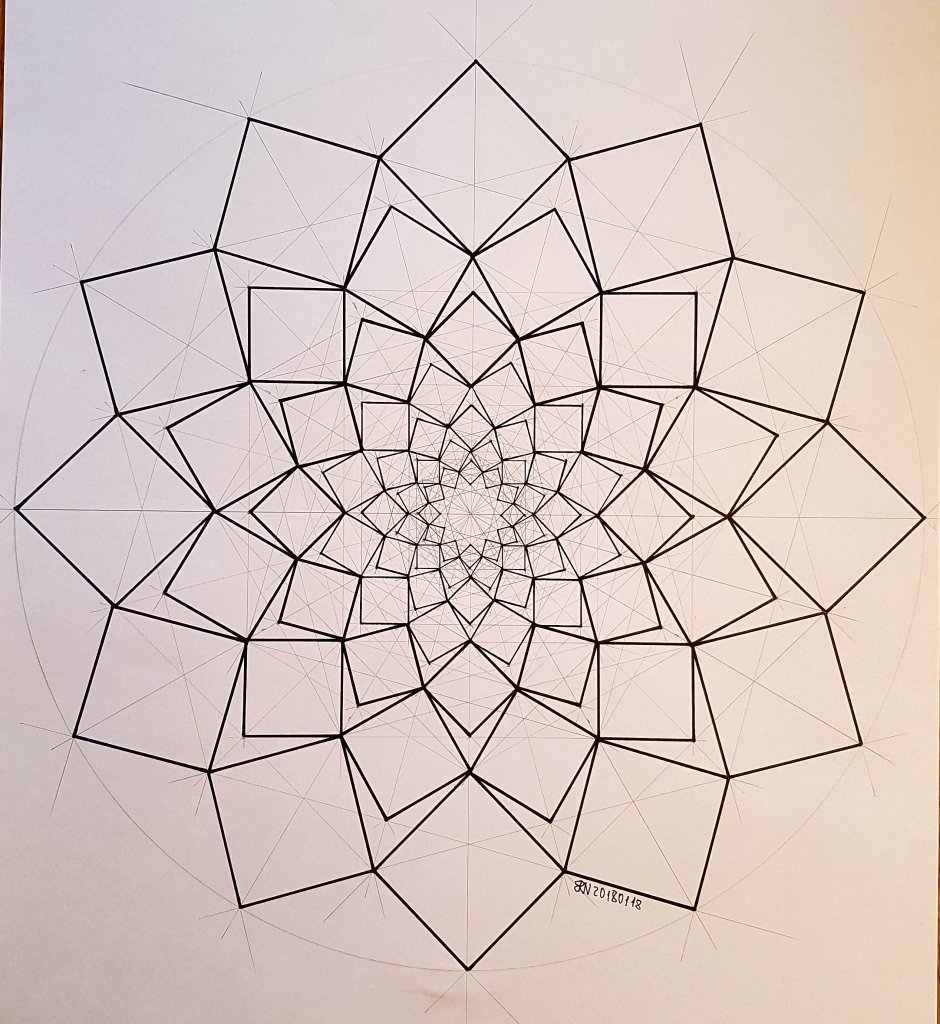
Fractal geometry
Fractal geometry, a mesmerizing branch of mathematics, unveils the hidden patterns and infinite complexity found in nature. Derived from the Latin word "fractus," meaning broken or fragmented, fractals are geometric shapes that exhibit self-similarity on various scales. These intricate formations can be observed in everything from snowflakes to coastlines, galaxies to trees.
With their intricate details and repeating patterns, fractals captivate our imagination and challenge our perception of reality. They possess a unique quality of never-ending complexity, where zooming into a section reveals a similar structure as the whole. This property is known as self-similarity, a concept that revolutionized the way we understand the world around us.
Not only are fractals aesthetically pleasing, but they also have practical applications in various fields. In physics, they aid in understanding the behavior of chaotic systems, such as weather patterns and fluid dynamics. Fractals also find their place in computer graphics, creating realistic landscapes and textures. Moreover, they have proven valuable in modeling biological structures like lungs and blood vessels.
The beauty of fractal geometry lies in its ability to bridge the gap between art and science. Artists and designers draw inspiration from fractals, incorporating their mesmerizing qualities into paintings and sculptures. Mathematicians and scientists, on the other hand, delve into the depths of fractal mathematics, unraveling its intricate mysteries.
In a world filled with straight lines and perfect shapes, fractals remind us of the inherent irregularity and infinite intricacy that surrounds us. They serve as a visual representation of chaos and order, blending the organic with the mathematical. So next time you gaze at a cloud or ponder a fern leaf, take a moment to appreciate the hidden wonders of fractal geometry.